Zero Events ≠ Declining Risk
Why “incident-free” streaks make systems fragile
Everyone knows this:
If something happens often, it’s relatively more likely to happen tomorrow.
If something happens rarely, it’s relatively less likely to happen tomorrow.
Years ago, in a metrics meeting, everyone knew that… except me.
Another week went by with no safety events.
I said something like “the likelihood of a safety incident happening next week is getting higher.”
People laughed. Are you joking, Frank? By definition, it’s the opposite.
And they were right, if you believe risk is constant.
By frequency counts or by Bayesian updating (which “everyone” indexes on), the probability goes down with every clean week.
But here’s the trap: zero events is not always equal to declining risk.
In many systems, I think risk accumulates.
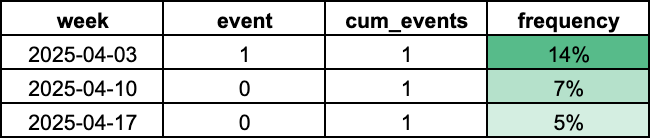
The simple way to perceive risk is frequency. Count the number of events, divide by the number of days.
The smaller the numerator, the smaller the rate.
That’s how everyone thinks.
So, the probability - like everyone knows - goes down when we don’t have incidents.
The Bayesian way is a little fancier. Start with a prior (say, the industry incident rate), then update it with what you’ve seen. If you’ve seen nothing, your estimated probability keeps nudging lower.
Both approaches agree: more clean days = lower estimated risk.
That’s the math1.
Makes sense… if risk is fixed.
But I don’t think it’s fixed.
Again, In many systems, I think risk accumulates.
Day after a safety briefing: people are alert. Risk is low.
Ten days later: habits loosen. Risk is a little higher.
Thirty days: almost nobody’s thinking about safety. Risk is peaking.
That “30 days incident-free” sign doesn’t make the warehouse safer.
It makes people feel immune.
That’s when the system becomes fragile.
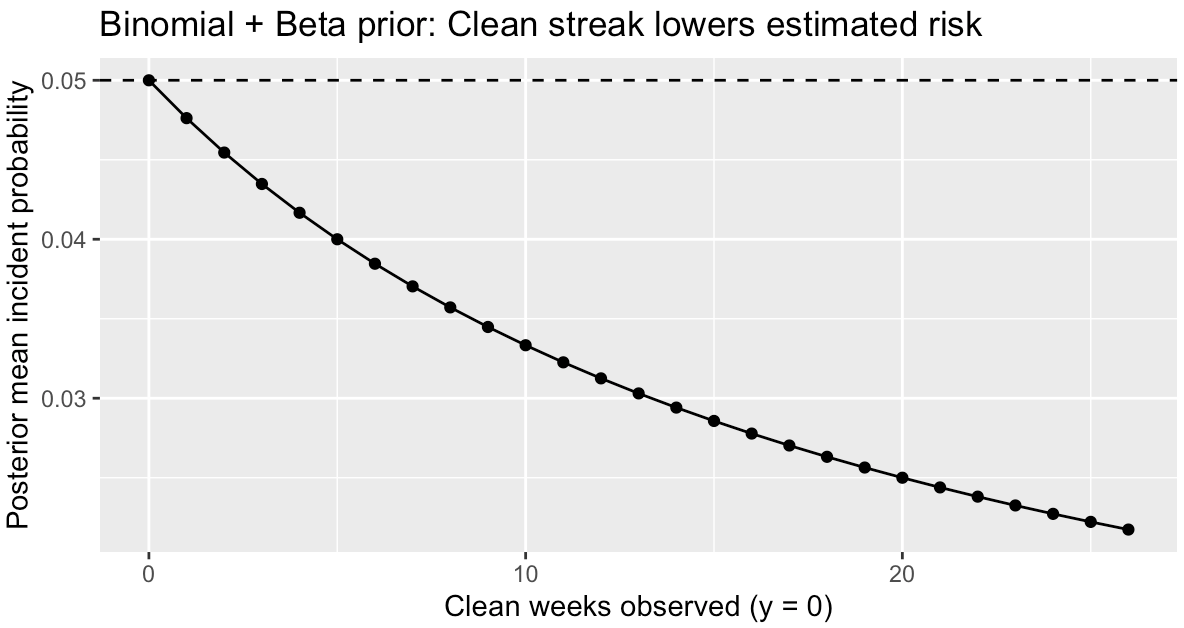
Mathematically, you can capture this intuition as:
where
𝑎 is days since the last “shock” (incident, audit, or training),
λ₀ is the risk level right after everyone is paying attention, and
k answers the question: how much more likely is trouble tomorrow if we go one more day without an event or intervention?2
The longer it’s been, the higher the probability creeps.
If you’re an eager analyst, take a read through this tutorial-esque R code.
If you’re only here for a minute, just internalize the idea with this chart:
The longer it’s been, the more complacent people get. And the more that “30 days incident-free” sign convinces them nothing will happen.
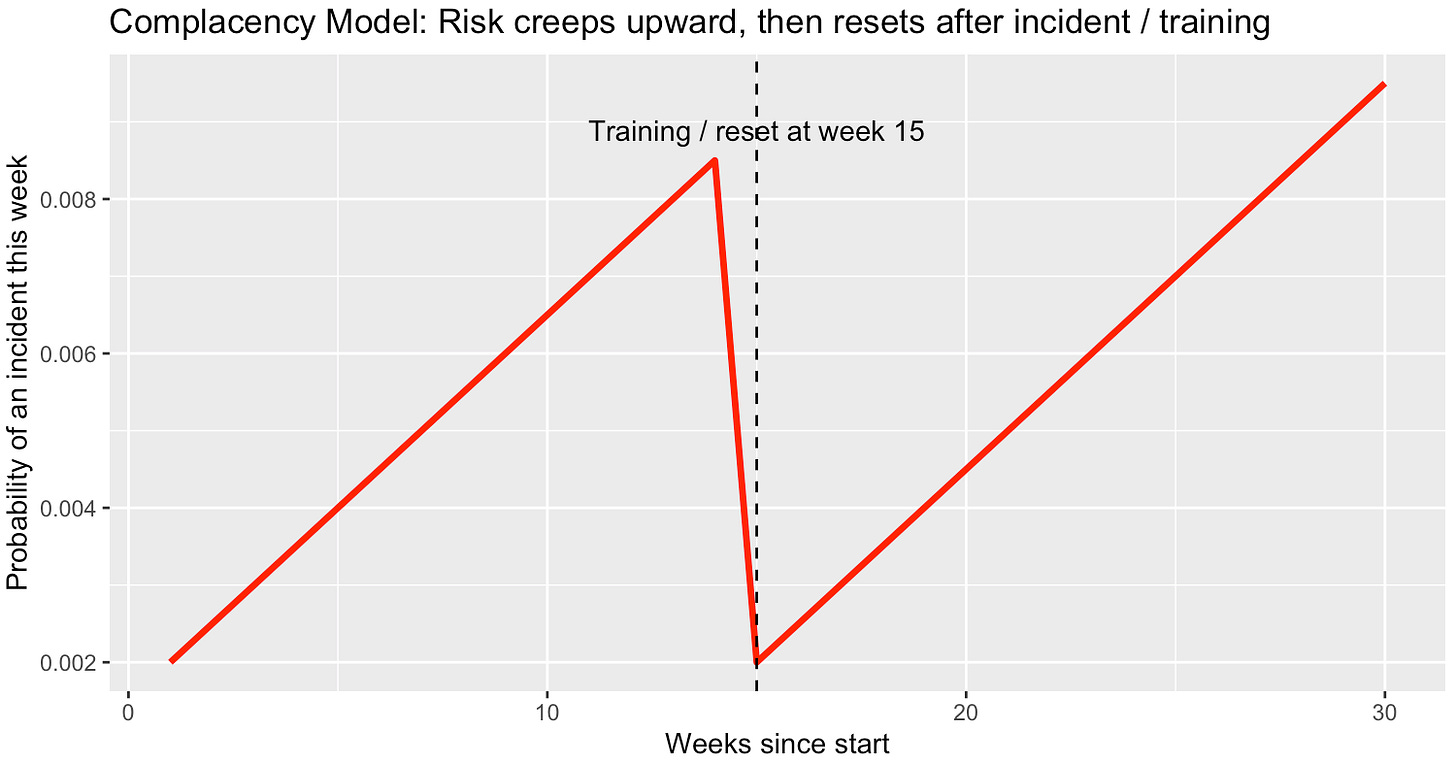
This is why the chart looks like a sawtooth: slow build, sharp reset.
Run a drill or a training, risk drops back down.
Skip it, and you’re winding a spring until it snaps.
Other examples of risk accumulation:
A dam with no maintenance in years.
A financial system with no stress tests.
Or Maui, 2023: a tinderbox created by overgrown brush, neglected infrastructure, and normalized “red flag” days. The absence of fire made people feel safe. Too safe, and then the whole town burned.
The same dynamic plays out with customers. If no tickets are coming in, is that good news? Maybe. Or maybe your users are disengaged, not pushing the product to its limits. Zero feedback doesn’t mean zero problems. It means you don’t have enough information, and you need to be talking with them constantly.
Back in that metrics meeting, I felt embarrassed for seeing it differently. Now I’m glad I do.
It means I can look at a “clean streak” and see it for what it is: not proof of safety, but a fragile system waiting for a reset. Calmness before the storm.
The real lesson?
The numbers alone won’t save you.
The way you analyze has to begin with the right framing of the world.
Get the framing wrong, and the math only takes you further off course.
Here’s a tutorial-esque Gist in R that you can read through.
There are at least two ways to estimate these parameters from your data: a descriptive linear model or a poisson survival model. This is good, but I think running the model with varying parameter values and using your intuition about the ballpark for those values is a fine starting point.

Interesting perspective - were you proven right in that specific case? Was it saw toothed like in the long run?